1. 为什么要使用进制
数据在计算机中的表示,最终以二进制的形式存在 , 就是各种《黑客帝国》电影中那些 0101010… 的数字 ;
我们操作计算机,实际就是使用程序和软件在计算机上各种读写数据,如果我们直接操作二进制的话 , 面对这么长的数进行思考或操作,没有人会喜欢。
进制越大,数的表达长度也就越短。
之所以使用16或8进制,而不其它的,诸如9或20进制,是因为2、8、16,分别是2的1次方、3次方、4次方。这一点使得三种进制之间可以非常直接地互相转换 ;
8进制或16进制 既 缩短了二进制数,还能 保持了二进制数的表达特点。转换还方便
2. 进制的介绍
- 进制是计算机中数据的一种表示方法。 N进制的数可以用0~(N-1) 的数表示, 超过9的用字母A-F 表示。
- 二进制
二进制是由 0-1 组成
- 八进制
八进制是由 0-7 组成
- 十进制
十进制就是我们日常所使用的数字,就是用 0~9 的数表示,逢 10 进 1
- 十六进制
十六进制是由 0-9, A-F 组成
与十进制的对应关系是: 0-9 对应 0-9, A-F 对应 10-15
字母不区分大小写
3. xx进制转换为十进制的转换公式
- 二进制转换为十进制
假设有一个二进制数:101100100, 转换为十进制为:356
使用横式计算(从右往左算)
0×20 + 0×21 + 1×22 + 0×23 + 0×24 + 1×25 + 1×26 + 0×27 + 1×28
0乘以任何数都是0,所以我们可以直接跳过值为0的数
1×22 + 1×25 + 1×26 + 1×28
4 + 32 + 64 + 256 = 356
- 八进制转换为十进制
假设有一个八进制数:1507, 转换为十进制为:839
使用横式计算(从右往左算)
7×80 + 0×81 + 5×82 + 1×83
0乘以任何数都是0,所以我们可以直接跳过值为0的数
7×80+ 5×82 + 1×83
7 + 320 + 512 = 839
- 十六进制转换为十进制
我们知道十六进制是由 0-9, A-F 组成,与十进制的对应关系是: 0-9 对应 0-9, A-F 对应 10-15,所以在进行十六进制转换为十进制的过程中如果遇到了A-F就把它转换为对应的数值再进行计算
假设有一个十六进制数:2AF5, 转换为十进制为:10997
使用横式计算(从右往左算)
5×160 + F×161 + A×162 + 2×163
将字母转换为对应的数值后
5×160 + 15×161 + 10×162 + 2×163
5 + 240 + 2560 + 8192 = 10997
- 十进制转换为十进制
假设有一个十进制数:1234, 转换为十进制为:1234
使用横式计算(从右往左算)
4×100 + 3×101 + 2×102 + 1×103
4 + 30 + 200 + 1000 = 1234
4. 通过 8421 方法快速将二进制转换为十进制的方法
首先我们来看一个二进制数:1111,它是多少呢?
你可能还要这样计算:1×2º+1×2¹+1×2²+1×2³ = 1×1+1×2+1×4+1×8 = 15。
我们必须直接记住1111每一位的权值,并且是从高位往低位记,:8、4、2、1。 即,最高位的权值为2³=8,然后依次是 2²=4,2¹=2,2º=1。
记住8 4 2 1,对于任意一个4位的二进制数,我们都可以很快算出它对应的10进制值。
接下来我们练习 通过 8421 的方式 进行 快速的计算 , 2,10,16进制的转换
1111 = 8 + 4 + 2 + 1 = 15 = F
1110 = 8 + 4 + 2 + 0 = 14 = E
1101 = 8 + 4 + 0 + 1 = 13 = D
1100 = 8 + 4 + 0 + 0 = 12 = C
1011 = 8 + 0 + 2 + 1 = 11 = B
1010 = 8 + 0 + 2 + 0 = 10 = A
1001 = 8 + 0 + 0 + 1 = 9 = 9
1000 = 8 + 0 + 0 + 0 = 8 = 8
0111 = 0 + 4 + 2 + 1 = 7 = 7
0110 = 0 + 4 + 2 + 0 = 6 = 6
0101 = 0 + 4 + 0 + 1 = 5 = 5
0100 = 0 + 4 + 0 + 0 = 4 = 4
0011 = 0 + 0 + 2 + 1 = 3 = 3
0010 = 0 + 0 + 2 + 0 = 2 = 2
0001 = 0 + 0 + 0 + 1 = 1 = 1
0000 = 0 + 0 + 0 + 0 = 0 = 0
8421方法一般用于二进制转16进制
5. 二进制转换为十六进制的方法
二进制转换为十六进制,就是以 4 位为一段,分别转换为十进制,然后再通过十进制推算出十六进制(因为十六进制是由 0-9, A-F 组成,与十进制的对应关系是: 0-9 对应 0-9, A-F 对应 10-15)
假设有一个二进制数:1111 1101 1010 0101 1001 1011, 转换为十六进制为:FDA59B
使用横式计算(从右往左算),计算出以 4 位为一段的十进制数
二进制: 1111 1101 1010 0101 1001 1011
通过8421方法快速计算出以为4位为一段的二进制的十进制数
十进制: 15 13 10 5 9 11
通过十六进制与十进制的映射关系推算出十六进制
十六进制: F D A 5 9 B
6. 十六进制转换为二进制的方法
假设有一个十六进制数:FDA59B , 转换为二进制为:1111 1101 1010 0101 1001 1011
通过十进制与十六进制的映射关系推算出十进制
十六进制: F D A 5 9 B
十进制: 15 13 10 5 9 11
通过8421方法反推出二进制数
二进制: 1111 1101 1010 0101 1001 1011
7. 十进制转换为二进制的方法
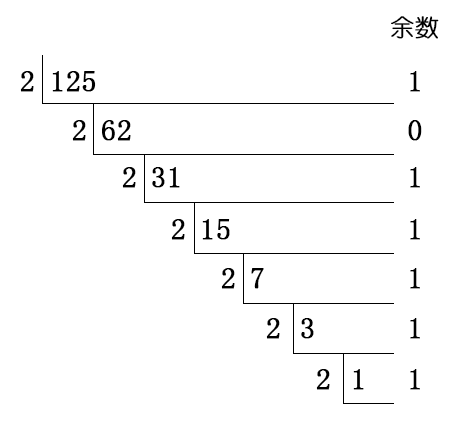
- 将一个十进制数除以2,得到的商再除以2,依此类推直到商等于0时为止,倒取除得的余数,即换算为二进制数的结果。只需记住要点:除2取余,倒序排列。
- 假设有一个十六进制数:125, 转换为二进制为:1111 101
125 ÷ 2 = 商:62 余:1
62 ÷ 2 = 商:31 余:0
31 ÷ 2 = 商:15 余:1
15 ÷ 2 = 商:7 余:1
7 ÷ 2 = 商:3 余:1
3 ÷ 2 = 商:1 余:1
1 ÷ 2 = 商:0 余:1
8. 十进制转换为十六进制的方法
- 将一个十进制数除以16,得到的商再除以16,依此类推直到商等于0时为止,倒取除得的余数,然后将大于9的余数通过十进制与十六进制的映射关系转换为英文字母 A-F,即换算为十六进制数的结果。只需记住要点:除16取余,将大于9的余数转换为英文,倒序排列。
- 假设有一个十六进制数:487710, 转换为十六进制为:7711E
487710 ÷ 16 = 商:30481 余:14(E)
30481 ÷ 16 = 商:1905 余:1
1905 ÷ 16 = 商:119 余:1
119 ÷ 16 = 商:7 余:7
7 ÷ 16 = 商:0 余:7

← 运行效率 进程 - 生产者消费者模型 →